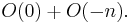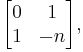Hirzebruch surface

In mathematics, a Hirzebruch surface is a ruled surface over the projective line. They were studied by Friedrich Hirzebruch (1951).

Definition

The Hirzebruch surface Σ_n is the P¹ bundle over P¹ associated to the sheaf

The notation here means: O(n) is the n-th tensor power of the Serre twist sheaf O(1), the invertible sheaf or line bundle with associated Cartier divisor a single point. The surface Σ₀ is isomorphic to P¹×P¹, and Σ₁ is isomorphic to P² blown up at a point so is not minimal.

Properties

Hirzebruch surfaces for n>0 have a special rational curve C on them: The surface is the projective bundle of O(-n) and the curve C is the zero section. This curve has self-intersection number −n, and is the only irreducible curve with negative self intersection number. The only irreducible curves with zero self intersection number are the fibers of the Hirzebruch surface (considered as a fiber bundle over P¹). The Picard group is generated by the curve C and one of the fibers, and these generators have intersection matrix

so the bilinear form is two dimensional unimodular, and is even or odd depending on whether n is even or odd.

The Hirzebruch surface Σ_n (n > 1) blown up at a point on the special curve C is isomorphic to Σ_n-1 blown up at a point not on the special curve.

External links

• Manifold Atlas

References

• Barth, Wolf P.; Hulek, Klaus; Peters, Chris A.M.; Van de Ven, Antonius (2004), Compact Complex Surfaces, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge., 4, Springer-Verlag, Berlin, ISBN 978-3-540-00832-3, MR2030225 
• Beauville, Arnaud (1996), Complex algebraic surfaces, London Mathematical Society Student Texts, 34 (2nd ed.), Cambridge University Press, ISBN 978-0-521-49510-3; 978-0-521-49842-5, MR1406314 
• Hirzebruch, Friedrich (1951), "Über eine Klasse von einfachzusammenhängenden komplexen Mannigfaltigkeiten", Mathematische Annalen 124: 77–86, doi:10.1007/BF01343552, ISSN 0025-5831, MR0045384